拓扑排序

这篇博客将向大家介绍如何利用拓扑排序判断一个有向图是否有环。

题面：

题目描述

在一个有向图中，判断是否存在一个简单有向回路

输入

输入第一行为n和m，表示n个顶点，m条边，接下来有m行，每行vi和vj，表示从vi到vj有一条弧

输出

输出文件为一行，若图中有简单有向回路，则输出“circle”，若没有，则输出“no circle”

我将向大家展示如何不用任何STL完成这道题（主要是忘了怎么用233）

在此特别感谢张怡和巨佬的友情帮助（花了一个小时帮我改bug）

废话不多说，正式开始题解

第一步是建树，用邻接表来做 邻接表有四样写法，你知道么，这个就不多说了，直接上代码吧，我用的是超级容易错的结构体指针。

struct node {
    int v;       //指向的节点
    node *next;  //下一条边
    node() {
        v = -1;
        next = NULL;
    }
} * head[1000];  //邻接表

void set() {
    for (int i = 1; i <= n; i++) head[i] = new node;
    for (int i = 1; i <= m; i++) {
        int x, y;
        cin >> x >> y;
        p[y]++;
        if (head[x]->v == -1) {  //是空节点
            head[x]->v = y;
        } else {
            node *pnew = new node;
            pnew->v = y;
            pnew->next = head[x];
            head[x] = pnew;
        }  //插入新的节点
    }
}

然后就是这道题的核心——用拓扑排序判断是否有环了。

首先介绍一下拓扑排序（来自百度百科，可以不看）：对一个有向无环图(Directed Acyclic Graph，简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边(u,v)∈E(G)，则u在线性序列中出现在v之前。通常，这样的线性序列称为满足拓扑次序(Topological Order)的序列，简称拓扑序列。简单的说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。

说人话就是：把一个有向无环图的所有节点按照某种顺序排列，使得所有节点指向的节点都在这个节点之后

还是看不懂的话看这个图就懂了：

假设这是神犇Mr_Wu某一天的时间规划表（若节点A指向节点B则表明Mr_Wu做节点B这件事前必须先做节点A中的事，如Mr_Wu在刷黑题之前必须提交检讨书解封）

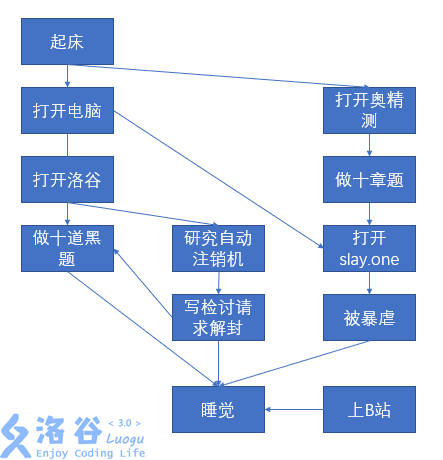
那么我们这时用拓扑排序算法就能很容易地帮助Mr_Wu把一天要做的事情排个序，排序结果如下图（排序方法不唯一）

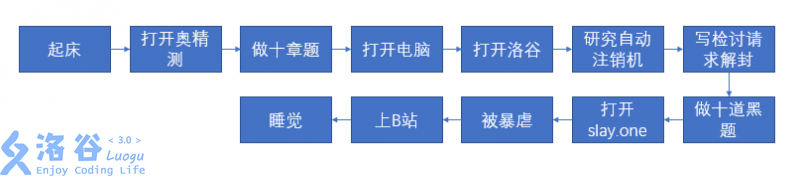
说完拓扑排序的功能，现在来说一下算法的实现。

我们来观察一下这副图，不难发现如果A指向B，那么做B这件事的条件就是完成A。我们可以把每条指向B的边都看做B的先决条件，有多少条边指向B，即B入度为几，做B这件事就有几个条件。

我们要做的第一件事一定是不需要做任何其他事情就能直接做的，换句话来说，就是入度为0的节点。我们发现，不需要做任何事情就可以起床，即“起床”这个节点的入度入度为零。我们就可以把“起床”放在我们时间规划表的第一项了。

所以拓扑排序的第一步就是要在所有的节点当中搜索入度为0的节点，放在排序结果数组的第一项。

Mr_Wu起床之后不做任何其他事情就可以打开电脑或奥精测了，这时，我们可以发现“打开电脑”和“打开奥精测”这两个节点都没有先决条件了，但是这两个节点的入度并不为零，这是因为指向这两个节点的“起床”节点已经完成，那么“起床”指向“打开电脑”的这条边就不再是“打开电脑”的先决条件了，所以我们可以把这条边看成一条“失效的”边。

我们就可以把“起床”指向“打开电脑”与指向“打开奥精测”的这两条“失效的”边删除了。而“起床”这件事已经做过，而且它的所有边都已被删除，所以我们就可以把“起床”这个节点一并删除。

拓扑排序的第二步即为把做过的节点与所有以做过的节点为起点的边全部删除。

删除后这个图就变成了这样：

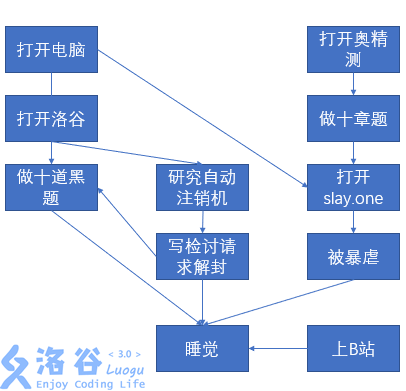
这时我们发现“打开电脑”和“打开奥精测”两个节点的入度都是0了，我们可以任选其一，将它加入时间规划表的第二项，并删除那个节点和以那个节点为起点的边。

接下来便重复上一步的动作，以此类推，直到把所有的节点都加入时间规划表中即可。

那么是否有优化的方法呢？答案是：当然有。

我们发现，上面的算法每次都要遍历一遍所有的节点，查找入度为0的节点，十分浪费时间。所以我们可以建立一个队列（队列我还是没有用STL），在最开始进行一次遍历，存储所有边的入度，并将所有入度为零的节点入队，然后每次都删除队首的节点，并在删除边时直接统计每条边的入度，并把入队为零的节点入队即可。

那说了这么多，拓扑排序到底和判断一个有向图是否有环有何关系呢？没有关系

再来看一眼我刚才粘上来的百度百科：对一个有向无环图(Directed Acyclic Graph，简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边(u,v)∈E(G)，则u在线性序列中出现在v之前。通常，这样的线性序列称为满足拓扑次序(Topological Order)的序列，简称拓扑序列。简单的说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。

注意加粗的部分，拓扑排序就是把一个有向无环图排列成拓扑序列。换句话说，一个有环图就无法通过拓扑排序把所有的节点排成拓扑序列。

举个栗子，Mr_Wu由于在学完数学后十分劳累，所以他决定刷几道黑题放松一下。但他由于使用自动注销机注销了自己，被洛谷封号，所以他需要写检讨来解封，但他太累了以至于必须要刷几道黑题来放松一下……

那么“写检讨”和“刷黑题”两个节点就形成了一个环。这两个节点的入度都是1.永远不会有一个节点会完成。那么如果这幅图（即这两个节点）是另一幅图的子图，那么另一个图拓扑排序结束后（入度为零的队列为空）这两个节点将不会被排序进拓扑序列中。

所以我们可以用一个变量来记录现在拓扑序列中的节点的个数，如果排序后节点个数等于图中的节点个数，即图中的所有节点都在拓扑序列中，那么这个图就没有环。如果拓扑序列中的节点的个数小于图中的节点数，那么就说明这幅图有环。

那么上代码吧：

#include <iostream>
using namespace std;
int n, m, p[10000] = {0};
struct node {
    int v;       //指向的节点
    node *next;  //下一条边
    node() {
        v = -1;
        next = NULL;
    }
} * head[1000];  //邻接表

void set() {  //建图
    for (int i = 1; i <= n; i++) head[i] = new node;
    for (int i = 1; i <= m; i++) {
        int x, y;
        cin >> x >> y;
        p[y]++;
        if (head[x]->v == -1) {  //是空节点
            head[x]->v = y;
        } else {
            node *pnew = new node;
            pnew->v = y;
            pnew->next = head[x];
            head[x] = pnew;
        }  //插入新的节点
    }
}
int topsort() {  //拓扑排序
    int queue[1000] = {0}, front = 0, rear = 0, cnt = 0;
    for (int i = 1; i <= n; i++) {
        if (p[i] == 0) {
            queue[rear++] = i;
        }
    }                        //第一次遍历
    while (front != rear) {  //队列不为空
        int m = queue[front++];
        if (m == 0) {
            break;
        }  // m为队首，即要删除的节点的编号
        node *a = head[m];
        while (1) {
            if (--p[a->v] == 0) {
                queue[rear++] = a->v;
            }                          //删边后入度为0的节点入队
            if (a->next == NULL) {     //到头了
                head[m]->next = NULL;  //删除节点
                cnt++;
                break;
            }
            a = a->next;  //下一条边
        }
    }
    return cnt;
}
int main() {
    cin >> n >> m;
    set();
    if (topsort() < n) {
        cout << "circle";
    } else {
        cout << "no circle";
    }
    return 0;
}