Muddy Fields G 题解

题目链接

首先有一个显然的事实，就是一块木板在延伸到最长的情况下一定是更优的。

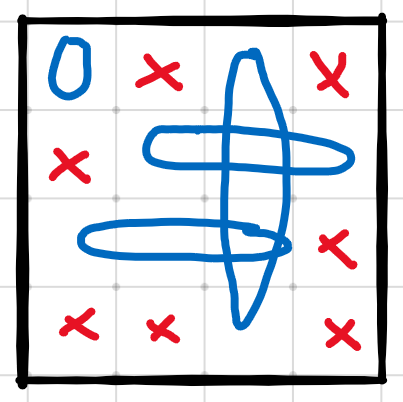
如图所示，覆盖 $(2,2),(2,3),(2,4)$ 的木板一定会优于仅覆盖 $(2,2),(2,3)$ 的木板，所以此题只需要考虑使用能延伸到最长的木板即可。也就是说，此题木板可能存在的位置是确定的，就是每行的连通块和每列的连通块，如图所示：

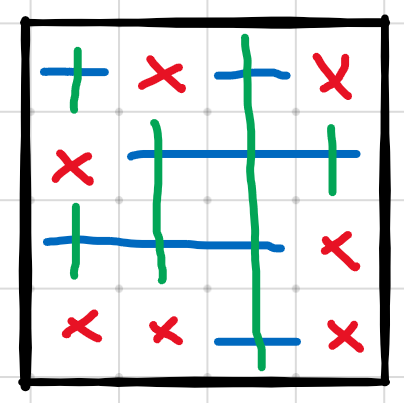
蓝线和绿线是木板可能存在的位置。

对于每个泥泞的格子，都至少要被自己所在的行连通块或列连通块的其中一个覆盖。让人情不自禁地想到二分图的最小点覆盖 ^[1]。

考虑把行连通块和列连通块分别看作左部节点和右部节点，每个泥泞的格子看作一条边，连接这个格子所在的行连通块和列连通块。那么这个二分图的最小点覆盖就是答案。

由 Konig^[2] 定理，只需求出该二分图的最大匹配即可。

代码：

#include <bits/stdc++.h>
using namespace std;
int n, m, b1[105][105], b2[105][105], num1, num2, vis[10005], match[10005], ans = 0;
// b1 表示所在行联通块编号，b2 表示所在列连通块编号
vector<int> head[10005];

bool dfs(int x) {
    for (auto q : head[x]) {
        if (!vis[q]) {
            vis[q] = 1;
            if (!match[q] || dfs(match[q])) {
                match[q] = x;
                return true;
            }
        }
    }
    return false;
}
// 匈牙利算法

char c[105][105];
signed main() {
    cin >> n >> m;
    for (int i = 1; i <= n; ++i)
        scanf("%s",c[i] + 1);

    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {
            if (c[i][j] == '*') num1++;
            while (c[i][j] == '*') b1[i][j] = num1, ++j;
        }
    } // 找行连通块

    for (int i = 1; i <= m; ++i) {
        for (int j = 1; j <= n; ++j) {
            if (c[j][i] == '*') num2++;
            while (c[j][i] == '*') b2[j][i] = num2, ++j;
        }
    } // 找列连通块

    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= m; ++j)
            if (c[i][j] == '*') head[b1[i][j]].push_back(b2[i][j]);
    // 建图

    for (int i = 1; i <= num1; ++i) {
        memset(vis, 0, sizeof(vis));
        ans += dfs(i);
    }
    // 匈牙利算法

    printf("%d\n", ans);
    return 0;
}