逃离地球的博客

图论学习笔记

图论学习笔记
2020-02-25 · 17 min read
学习笔记

最近本蒟蒻在复习图论，发现自己已经基本把图论给忘了，所以就打算写这样一篇学习笔记，用来复习。

一、图的表示

1.邻接矩阵

用一个二维数组存边，map[i][j]=kmap[i][j]=k表示点ii到点jj权值为kk。添边、查边复杂度都是O(1)O(1)，访问所有与一个点连接的点的复杂度为O(n)O(n)，占用空间较大，适合稠密图。
模板：

int G[5000][5000], u, v, k, n, m;
scanf("%d%d", &n, &m);
for (int i = 0; i < m; ++i) {
	scanf("%d%d%d", &u, &v, &k);
	G[u][v] = k;
}

2.邻接表

用nn个数组存储每个节点发出的边，占用空间较小，适合稀疏图。

模板（vector方法）：

#include<bits/stdc++.h>
using namespace std;

struct Node {
	int v, k;
};
vector<Node> head[5000];

int main() {
	int n, m, u, v, k;
	scanf("%d%d", &n, &m);
	for (int i = 0; i < m; ++i) {
		scanf("%d%d%d", &u, &v, &k);
		head[u].push_back((Node) {v, k});
	}
	return 0;
}

二、拓扑排序

见这个博客

三、最小生成树

1.定义

一个无向连通图的最小生成树是该图的一个子图，且是一棵树，包含图中的所有顶点，且边权和最小。

2.Prim算法

设一个点集QQ中仅包含初始节点（可以是任意节点），寻找一条边(u,v)(u,v)，满足点uu在集合QQ中，点vv不在集合QQ中，且边权是所有这样的边中最小的，则这条边是最小生成树中的一条边，将点vv也加入集合QQ中，重复这样的操作，直到集合QQ中包含所有的节点。那么找到的所有的边的集合就是这个图的最小生成树。Prim算法主要利用了贪心的思路。

形象地说，就是在图上选一个点，然后在这个点的周围画一个圈。（如图）

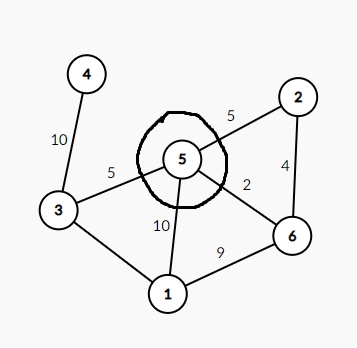
enter image description here

然后在和圈相交的边里面选一条权值最小的（在图中即5与6之间的边），再把这个权值最小的边指向的节点也围到圈里。（如图）

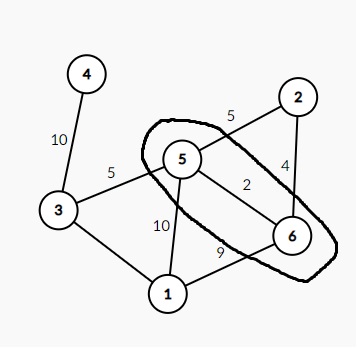
enter image description here

然后再找与圈相交的边权最小的边，并把指向的节点圈到圈里面，以此类推，直到圈里包含了所有的节点，那么所有选过的边就是这棵树的最小生成树。

模板：

#include<bits/stdc++.h>
using namespace std;
const int INF = 1e9;
struct Node {
    int v, k;
};
vector <Node> head[200002];

int q[200002], n, m, tot = 0; //q[i]表示点i是否在点集q中
priority_queue<pair<int, int> > p; //堆优化,记录节点i与点集q中一点相连的最短的边的权值

void Prim(int root) {
    p.push(make_pair(0, root));
    memset(q, 0, sizeof(q));

    int u, v, k;
    while (!p.empty()) {
        k = p.top().first, u = p.top().second;
        p.pop();

        if (q[u]) {
            continue;
        }//节点u已经在集合q中，直接跳过
        tot += k;
        q[u] = 1;

        for (int j = 0; j < (signed)head[u].size(); ++j) {
            v = head[u][j].v, k = head[u][j].k;
            if (!q[v]) {
                p.push(make_pair(k, v));
            }
        }//更新p数组
    }
}

int main() {
    scanf("%d%d", &n, &m);
    int x, y, z;
    for (int i = 1; i <= m; ++i) {
        scanf("%d%d%d", &x, &y, &z);
        head[x].push_back((Node) {y, -z});
        head[y].push_back((Node) {x, -z});
        //由于优先队列是大根堆，就把边权取反，即可变成小根堆
    }

    Prim(1);
    printf("%d\n", -tot);
    return 0;
}

3.Kruskal算法

首先将所有的节点放入不同的点集中，每个点集中只有一个节点。然后进行遍历，寻找一条边(u,v)(u,v)，满足节点uu与节点vv不在同一个集合中，且是满足这个条件的边中权值最小的。那么这条边就是最小生成树中的一条边。将节点uu与节点vv所在的集合合并，再进行查找边与合并集合的操作，直到所有的点都在同一个集合中，那么找到的所有的边的集合就是这个图的最小生成树。

Kruskal算法可以利用并查集实现。

形象地说，就是在图中所有的节点周围都画一个圈（如图）：

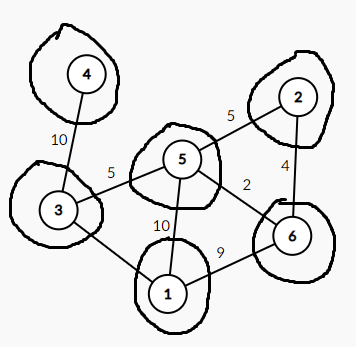
enter image description here

再在不被包含在一个圈里的的边（即与两个圈有交点的边）找到权值最小的边（在图中即5到6的边），把这两个圈合并。（如图）

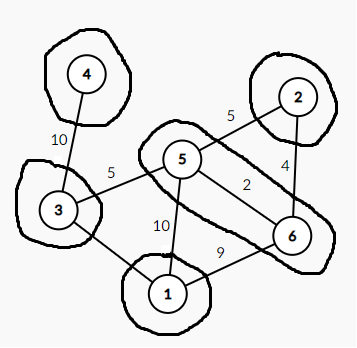
enter image description here

然后重复这样的操作，直到所有的节点都在一个圈里，那么所有选过的边就是这棵树的最小生成树。

模板：

#include<bits/stdc++.h>
using namespace std;
const int INF = 1e9;
int n, m, pre[200001], tot = 0, k = 0;

struct Node {
    int u, v, k;
};

vector<Node> edge;//edge数组存边

//----------------------------------------并查集
inline int find(int x) {
    int y = x, j;
    while (x != pre[x])
        x = pre[x];

    while (y != x) {
        j = pre[y];
        pre[y] = x;
        y = j;
    }
    return x;
}

inline void join(int x, int y) {
    int pre_x = find(x), pre_y = find(y);
    if (pre_x != pre_y) {
        pre[pre_x] = pre_y;
    }
}
//----------------------------------------并查集

bool cmp(Node x, Node y) {
    return x.k < y.k;
}

void Kruskal() {
    sort(edge.begin(), edge.end(), cmp); //将边按权值从小到大排序
    int cnt = 0;
    for (int i = 0; i < m; i++) {
        if (cnt == n - 1) {
            return;
        }//边够了
        int u = edge[i].u, v = edge[i].v, k = edge[i].k;
        if (find(u) != find(v)) { //如果这条边可以选
            join(u, v);
            cnt++;
            tot += k;
        }
    }
}

int main() {
    scanf("%d%d", &n, &m);
    int x, y, z;
    for (int i = 1; i <= m; i++) {
        scanf("%d%d%d", &x, &y, &z);
        edge.push_back((Node) {x, y, z});
    }

    for (int i = 1; i <= n; i++) {
        pre[i] = i;
    }//并查集初始化

    Kruskal();
    printf("%d\n", tot);
    return 0;
}

4.Prim算法与Kruskal算法的区别

算法 Prim Kruskal
时间复杂度 O(v∗log(v))O(v*log(v)) O(e∗log(e))O(e*log(e))
适用范围 稠密图 稀疏图

注：vv为点数，ee为边数。
Prim算法需要通过堆优化后复杂度才能达到O(v∗log(v))O(v*log(v))。

四、最短路

1.定义

最短路问题（short-path problem）是网络理论解决的典型问题之一，可用来解决管路铺设、线路安装、厂区布局和设备更新等实际问题。基本内容是：若网络中的每条边都有一个数值（长度、成本、时间等），则找出两节点（通常是源节点和阱节点）之间总权和最小的路径就是最短路问题。——百度百科

说人话就是在选一条连接两个点的路径，使这条路权值和最小。

2.Dijkstra算法

Dijkstra算法是一个求单源最短路径的算法，只适用于没有负权边的图。Dijkstra算法与Prim算法有些类似，都是设一个点集QQ，最初只有一个节点，然后不断地添点，直到全部添加。

设点集QQ，最初只包含起点uu。设dis[i]dis[i]为目前找到的uu点到编号为ii的节点的最短路径，所有dis[i]dis[i]初始化为INF，dis[u]dis[u]初始化为00。首先寻找不在点集中且disdis值最小的点xx，将点xx加入QQ中，并进行松弛操作，即对于所有从xx点出发的边(x,y)(x,y)，dis[y]=min(dis[y],dis[x]+w(x,y))dis[y]=min(dis[y],dis[x]+w(x,y)).然后再进行找点，加点与松弛的操作，直到所有点都被加入QQ中为止。那么最短路就求出来了。

原理是由于图中没有负边，所以如果dis[i]dis[i]为图中最小的，那么它就不可能再被更新，所以就可以被确定，即被加入点集QQ中。

如果需要记录路径，那么就建立一个father[n]father[n]数组，father[i]father[i]表示ii节点的上一个节点。每次进行松弛操作时，如果dis[i]>dis[j]+w(i,j)dis[i]>dis[j]+w(i,j)，那么就将father[i]father[i]赋值为jj即可。

与Prim算法相似，Dijkstra算法也可以在找disdis值最大的节点时利用堆进行优化。

模板：

#include<bits/stdc++.h>
using namespace std;
const int INF = 1e9;
struct Edge {
    int v, k;
};
vector<Edge> head[100001];

int dis[100001], q[100001];

struct Node {
    int dis, u; //u:节点编号 dis:dis值
    bool operator<(const Node& a) const { //运算符重载，以使用STL优先队列
        return dis > a.dis;
    }
};

int n, m;
void Dijkstra(int s) {
    priority_queue<Node> que;//堆优化
    bool vis[100001] = {0}; //是否被访问过
    memset(dis, 0, sizeof(dis));
    dis[s] = 0;
    que.push((Node) {0, s});
    while (!que.empty()) {
        int u = que.top().u;
        que.pop();
        if (vis[u]) { //如果已经被访问过了，那么这个节点的dis值就是在松弛操作之前的dis值了，直接删除即可。
            //由于松弛后的dis值一定小于松弛前的dis值，所以不用担心出错。
            continue;
        }
        vis[u] = 1;
        q[u] = 1;
        for (int i = 0; i < (signed)head[u].size(); i++) {
            int v = head[u][i].v, k = head[u][i].k;
            if (!q[v] && dis[v] > dis[u] + k) { //松弛操作
                dis[v] = dis[u] + k;
                que.push((Node) {dis[v], v});
            }
        }
    }
}

int main() {
    int u, v, k, s;
    scanf("%d%d%d", &n, &m, &s);

    for (int i = 0; i < m; i++) {
        scanf("%d%d%d", &u, &v, &k);
        head[u].push_back((Edge) {v, k});
    }
    Dijkstra(s);
    for (int i = 1; i <= n; i++) {
        printf("%d ", dis[i]);
    }
    return 0;
}

3.Bellman-Ford算法

Bellman-Ford算法可以求有负权边的图的单源最短路径。算法是对disdis数组进行n−1n- 1（n 为节点个数）轮松弛操作。

原理是最短路一定经过n−1n-1个节点（起点不算），即有n−1n-1个disdis值需要更新。每更新一个节点的disdis值，其他的节点也可能会受到影响。故进行n−1n-1轮松弛操作后可以保证求出最短路。

模板：

#include<bits/stdc++.h>
using namespace std;
const int INF = 1e9;
struct Node {
    int u, v, k;
};
vector <Node> edge;

int dis[100001];

int n, m;
void Bellman_Ford(int s) {
    memset(dis, 0, sizeof(dis));
    dis[s] = 0;
    for (int i = 0; i < n - 1; i++) {
        for (int j = 0; j < m; j++) {
            int u = edge[j].u, v = edge[j].v, k = edge[j].k; //遍历每一条边，进行松弛
            if (dis[v] > dis[u] + k) {
                dis[v] = dis[u] + k;
            }
        }
    }
}

int main() {
    int u, v, k, s;
    scanf("%d%d%d", &n, &m, &s);

    for (int i = 0; i < m; i++) {
        scanf("%d%d%d", &u, &v, &k);
        edge.push_back((Node) {u, v, k}); //edge数组存边
    }
    Bellman_Ford(s);
    for (int i = 1; i <= n; i++) {
        printf("%d ", dis[i]);
    }
    return 0;
}

另外值得一提的是Bellman-Ford算法还可以判断图中是否存在负环（即权值和为负的环），只需要在进行n-1次操作后再进行一轮松弛操作，如果还有节点的disdis值被更新，说明图中存在负环。

4.SPFA算法

它不是死了吗
Shortest Path Fast Algorithm 算法是Bellman-Ford算法的队列优化版本。

我们可以发现，如果一个点的disdis值更新了 ，那么与这个节点相邻的节点的disdis值都可能会受到影响。所以我们可以建一个队列，存放等待更新的节点，并每次对队首的节点进行松弛操作并把所有与队首相连的节点入队，并把队首pop出去，重复进行这样的操作，直到队列为空。

模板：

#include<bits/stdc++.h>
using namespace std;
const int INF = 10e9;
int n, m, dis[100001];
struct Node {
    int v, k;
};
vector<Node>head[100001];

void SPFA(int s) {
    bool vis[100001];//vis数组记录是否在队列中
    queue<int> que;
    que.push(s);
    for (int i = 0; i <= n; i++) {
        dis[i] = INF;
        vis[i] = 0;
    }
    vis[s] = 1;
    dis[s] = 0;

    while (!que.empty()) {
        int num = que.front();
        que.pop();
        vis[num] = 0;
        for (int i = 0; i < head[num].size(); i++) { //对队首进行松弛操作
            if (dis[head[num][i].v] > dis[num] + head[num][i].k) {
                dis[head[num][i].v] = dis[num] + head[num][i].k;
                if (!vis[head[num][i].v]) { //如果队首更新，就把与队首相邻的节点入队
                    que.push(head[num][i].v);
                    vis[head[num][i].v] = 1;
                }
            }
        }
    }
}

int main() {
    int s, x, y, z;
    Node a;
    scanf("%d%d%d", &n, &m, &s);
    for (int i = 1; i <= m; i++) {
        scanf("%d%d%d", &x, &y, &z);
        head[x].push_back((Node) {y, z});
    }
    SPFA(s);
    for (int i = 1; i <= n; i++) {
        printf("%d ", dis[i]);
    }
    return 0;
}

5.Floyd-Warshall算法

Floyed-Warshall算法可以求出多源最短路径，即求出任意两点之间的最短路径。Floyd-Warshall算法的本质是动态规划。设disk[i][j]dis_{k}[i][j]表示节点ii和节点jj之间的一条仅经过编号最大不超过kk的节点最短路径的长度，那么显然dis0[i][j]=w(i,j)dis_{0}[i][j]=w(i,j)，因为kk=0，所以路径中不能经过其他节点。

那么如何从disk−1[i][j]dis_{k-1}[i][j]推出disk[i][j]dis_{k}[i][j]呢？我们需要分两种情况：

  1. disk[i][j]dis_{k}[i][j]是一条不经过kk节点的路径的长度，那么disk[i][j]=disk−1[i][j]dis_{k}[i][j]=dis_{k-1}[i][j].
  2. disk[i][j]dis_{k}[i][j]是一条经过ii节点的路径的长度，那么disk[i][j]=disk−1[i][k]+disi−1[k][j]dis_{k}[i][j]=dis_{k-1}[i][k]+dis_{i-1}[k][j] (将这条路径分为两部分)

由此我们可以得到状态转移方程：
disk[i][j]=max(disk−1[i][j],disk−1[i][k]+disk−1[k][j])dis_{k}[i][j]=max(dis_{k-1}[i][j],dis_{k-1}[i][k]+dis_{k-1}[k][j])

模板：

#include<bits/stdc++.h>
using namespace std;
const int INF = 1e9;
int n, dis[1001][1001];

void Floyd_Warshall() {
    for (int k = 1; k <= n; k++) { //循环k的值
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                if (dis[i][k] != INF && dis[k][j] != INF && dis[i][k] + dis[k][j] < dis[i][j]) { //状态转移
                    dis[i][j] = dis[i][k] + dis[k][j];
                }
            }
        }
    }
}

int main() {
    scanf("%d", &n);
    int x, y, z;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            scanf("%d", &dis[i][j]);
            if (dis[i][j] == -1) {
                dis[i][j] = INF;
            }
        }
    }//邻接矩阵存图

    Floyd_Warshall();

    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            if (dis[i][j] == INF)
                printf("-1 ");
            else
                printf("%d ", dis[i][j]);
        }
        printf("\n");
    }
    return 0;
}

update on 2019/11/12:改变了码风，修改了一些错误，Prim算法增加了堆优化。

本站总访问量次