并查集学习笔记

2020-03-09 · 8 min read

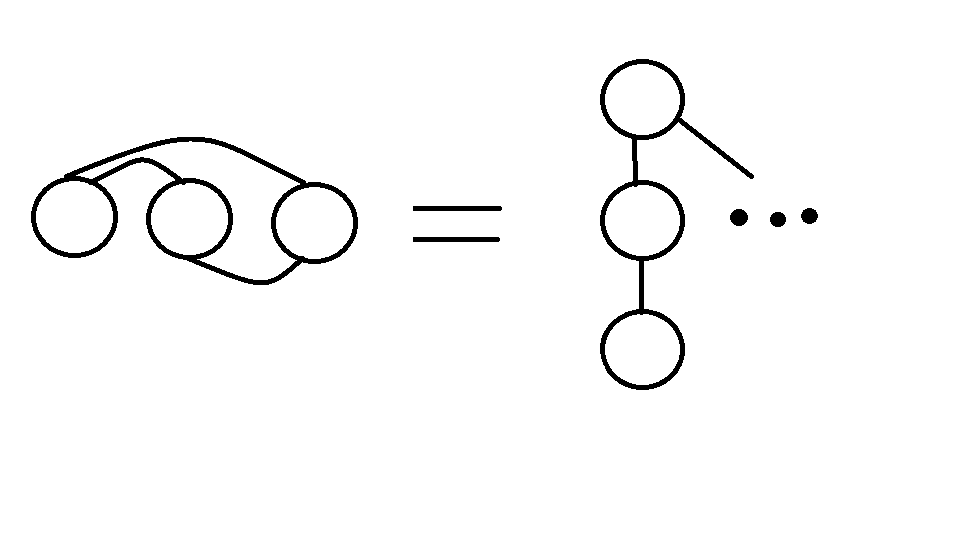
此博客主要介绍并查集的扩展域与边带权算法，参考《算法竞赛进阶指南》一书，把书中我第一遍读的时候不太理解的内容用自己的话写出来。

并查集

代码

int get(int x) { return (x == fa[x]) ? x : fa[x] = get(fa[x]); }
void insert(int x, int y) { fa[get(x)] = get(y); }

//main 函数里
for (int i = 1; i <= n; ++i) fa[i] = i;

扩展域

用于维护某种关系的传递。

例一：

有 $n$ 个数，每次告诉你某两个数的奇偶性是否相同，如果与前面的条件矛盾就把这个条件视为无效，问共有多少个条件与前面的条件矛盾。

题解：

考虑把每个数拆成两个节点，设第 $i$ 个数 $a_i$ 的两个节点为 $i_1$ 与 $i_2$ 。我们把这两个节点视作 $a_i$ 的奇偶性的两种情况。我们把两点之间连的边视为「这两个奇偶性在一种情况内出现」。

若 $a_i$ 和 $a_j$ 奇偶性相同，因为 $a_i$ 奇与 $a_j$ 奇一定同时发生， $a_i$ 偶 $a_j$ 偶一定同时发生，就把 $i_1$ 与 $j_1$ , $i_2$ 与 $j_2$ 连边；同理，若奇偶性不同，就把 $i_1$ 与 $j_2$ , $i_2$ 与 $j_1$ 连边。

显然任意数 $a_i$ 的两个点 $i_1$ 和 $i_2$ 在两个不同的连通块内，若 $i_1$ 与 $j_1$ 在同一连通块内，说明在 $a_i$ 为奇时 $a_j$ 也为奇， $a_i$ 为偶时反之，即 $a_i$ 与 $a_j$ 奇偶性相同。同理，若 $i_1$ 与 $j_2$ 在同一连通块内，则说明 $a_i$ 与 $a_j$ 奇偶性不同。

联通块的维护可以由并查集完成。由此方法判断奇偶关系，即可解决奇偶性的传递关系问题。

例二：食物链

题解：

考虑对于每个动物，别的动物对这个动物来说有三种可能的身份，即「同类」，「捕食者」（捕食这个动物的动物），「被捕食者」（被这个动物捕食的动物）。我们考虑把每个动物 $i$ 拆成 $3$ 个点 $i_1$ , $i_2$ , $i_3$ ，分别代表 $i$ 的同类、捕食者和被捕食者，并把相同的物种之间连边。

具体地说，若 $i$ 捕食 $j$ ，那么 $i$ 的同类就是 $j$ 的捕食者， $i$ 的捕食者就是 $j$ 的被捕食者， $i$ 的被捕食者就是 $j$ 的同类。就在 $i_1$ 和 $j_2$ , $i_2$ 和 $j_3$ , $i_3$ 和 $j_1$ 之间连边。同理，若 $i$ 与 $j$ 是同类，就在 $i_1$ 和 $j_1$ , $i_2$ 和 $j_2$ , $i_3$ 和 $j_3$ 之间连边。

此时，相同的物种就在相同的连通块内，询问两个动物的关系时，判断这两个动物的的「同类」，「捕食者」，「被捕食者」所处的连通块的关系即可。

代码：

#include <bits/stdc++.h>
using namespace std;
inline int read() {
    int ret = 0, f = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9') f = (ch == '-') ? -f : f, ch = getchar();
    while (ch >= '0' && ch <= '9') ret = ret * 10 + ch - '0', ch = getchar();
    return ret * f;
}
int n, k, ans = 0, fa[160005];

int get(int x) { return (x == fa[x]) ? x : fa[x] = get(fa[x]); }
void insert(int x, int y) { fa[get(x)] = get(y); }

int query(int x, int y) {
    int x1 = get(x * 3), x2 = get(x * 3 + 1), x3 = get(x * 3 + 2),
        y1 = get(y * 3), y2 = get(y * 3 + 1), y3 = get(y * 3 + 2);
    if (x1 == y1 && x2 == y2 && x3 == y3) return 1;  // x 与 y 同类
    if (x1 == y2 && x2 == y3 && x3 == y1) return 2;  // x 捕食 y
    if (y1 == x2 && y2 == x3 && y3 == x1) return 3;  // y 捕食 x
    return 0;                                        // 暂无关系
}  // 询问 x 和 y 捕食关系

void modify(int x, int y, int op) {
    int x1 = 3 * x, x2 = 3 * x + 1, x3 = 3 * x + 2;
    int y1 = 3 * y, y2 = 3 * y + 1, y3 = 3 * y + 2;
    if (op == 1) insert(x1, y1), insert(x2, y2), insert(x3, y3);  // x 与 y 同类
    if (op == 2) insert(x1, y2), insert(x2, y3), insert(x3, y1);  // x 捕食 y
}  // 修改 x 和 y 的关系

signed main() {
    n = read(), k = read();
    int op, x, y, q;
    for (int i = 1; i <= n * 3 + 2; ++i) fa[i] = i;
    for (int i = 1; i <= k; ++i) {
        op = read(), x = read(), y = read();
        if (x > n || y > n || (op == 2 && x == y)) {
            ++ans;
            continue;
        }
        q = query(x, y);
        if (q != op && q != 0) {
            ++ans;
            continue;
        }
        if (!q) modify(x, y, op);
    }
    printf("%d\n", ans);
    return 0;
}

边带权

在实现并查集的同时维护距离信息。

例一：银河英雄传说

题解：

判断是否在同一列可以用并查集解决，但是询问两艘战舰之间的距离普通并查集无法做到。边带权即在维护并查集的同时记录该节点对应战舰和父亲节点对应战舰之间的距离。而当路径压缩后，父亲节点就是根节点，即对应队首战舰，那么距离信息就很方便统计了。代码如下：

int get(int x) {
    if (x == fa[x]) return x;
    int root = get(fa[x]);
    d[x] += d[fa[x]];
    // 此时父亲节点的父亲为根，那么父亲节点的距离信息就是父亲节点到根的距离
    // 该节点也将要路径压缩，则需要把距离信息也设为到根的距离
    // 显然该节点到根的距离为 d[x] + d[fa[x]]
    return fa[x] = root;
}

调用查询函数后， $x$ 节点到根节点的距离就是 $d[x]$ ，那么 $x$ 战舰与 $y$ 战舰的距离就是 $|d[x]-d[y]|-1$ .

还要完成合并操作，对于把 $A$ 列合并到 $B$ 列，就需要把 $A$ 列根节点的父亲节点设为 $B$ 列根节点，同时要把 $A$ 列根节点的距离信息设为 $B$ 列的大小（因为合并后 $A$ 列队首到 $B$ 列队首的距离就是 $B$ 列的大小），所以同时要在并查集的根节点处记录该列的大小。代码如下：

void merge(int x, int y) {
    x = get(x), y = get(y);
    fa[x] = y, d[x] = size[y];
    size[y] += size[x];
}

例二：

同「扩展域」例一。

题解：

此题还可以用边带权并查集来解决。距离信息记录该节点与父亲几点奇偶性是否相同，如果相同则为 $0$ ，否则为 $1$ .

查询操作与上题几乎相同，只需将 d[x] += d[fa[x]] 改为 d[x] ^= d[fa[x]] 即可。

修改操作有些不同。假设已知 $x$ 和 $y$ 的奇偶性关系，需要合并，设 $x$ 所在并查集的根节点是 $p$ , $y$ 所在并查集的根节点是 $q$ , $d[x]$ 是 $x$ 到 $p$ 的异或和， $d[p]$ 是 $p$ 到 $q$ 的异或和， $d[y]$ 是 $y$ 到 $p$ 的异或和。若 $x$ 与 $y$ 奇偶性相同，那么有，即 $d[p] = d[x] \operatorname{xor} d[y] \operatorname{xor} 0$ . 同理，若奇偶性不同，则 $d[p] = d[x] \operatorname{xor} d[y] \operatorname{xor} 1$ . 由此即可实现距离信息的维护。

- 并查集
  *