斜率优化学习笔记
此博客仅仅介绍斜率优化的概念,没有例题和代码,是入门内容。
考虑一道状态转移方程式形如
的动态规划题目,其中 和 都是递增的函数。
那么对于某一个 ,有 . 设直线 的解析式为 ,则该直线斜率为 ,截距为 。
考虑每一条直线 ,由于 该直线截距为 ,则该直线截距越小, 就越小。所以最小化 的问题就可以转化为在 中找出截距最小的一条,再解出对应的 即可。
同时,对于每一条直线 ,该直线都会过点 。所以求 其实也就是找到一个点 ,使得一条过这个点的、斜率为 的直线的截距最小。
总结一下,此时的解答策略就是对于 ,找到过所有已知点的斜率为 的直线中截距最小的,由此解出 ,然后再插入点 ,以此类推。
下面来讨论又没有一种情况,使得某一个点对于任意一个斜率来说都不会是最优解。
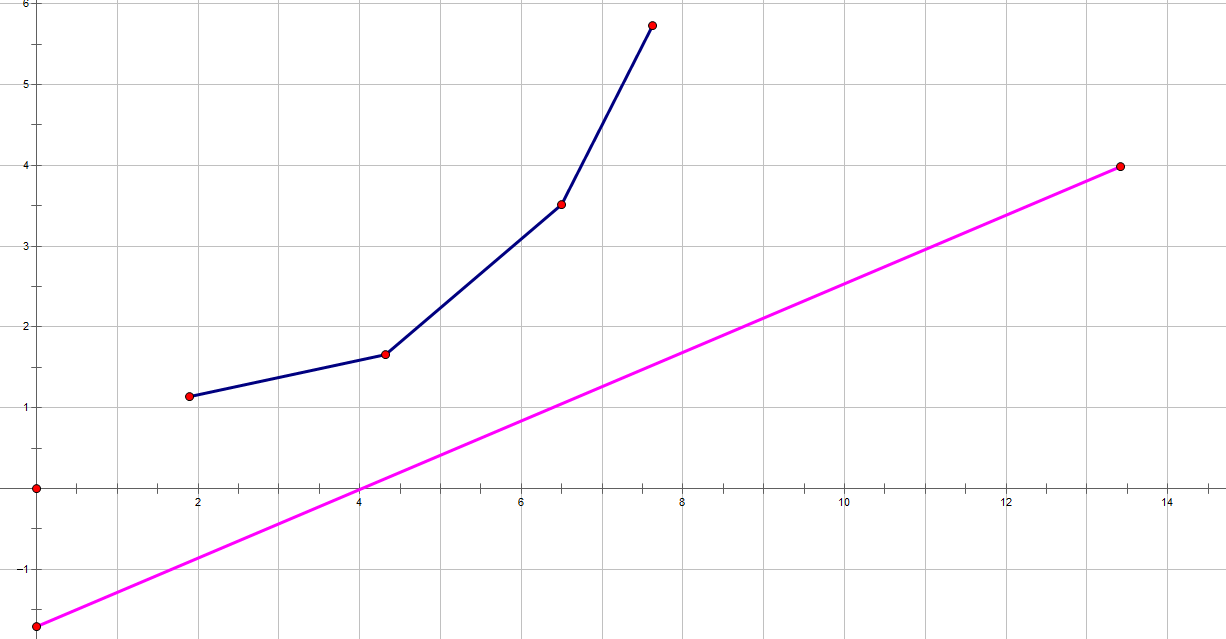
考虑这样的一个 点,显然,对于任意一条过 点的直线,都会至少有 点和 点中的一个点在该直线下方。那么经过该下方点的直线的截距就要小于过 点的直线的截距。故 点永远取不到最优解。
我们称这种情况为「上凸」。即直线 的斜率大于直线 的斜率,对于这样的 点,直接排除即可。
那么我们就只需要考虑这样的「下凸」的情况即可,称之为「下凸壳」。
如图,在下凸壳 上,如果点 满足 斜率小于 , 斜率大于 ,那么对于斜率为 的情况,过 的直线的截距是最小的,因为过其他点的直线一定都在 点上方。
那么寻找斜率为 时的最优解的问题就转化为了寻找一个点,使得这个点和前一个点的连线的斜率小于 ,这个点和后一个点的连线的斜率大于 的问题了。由于在下凸壳上,所以显然只有一个点满足条件。且若所有连线斜率均 大于/小于 当前要求斜率,那么 第一个/最后一个 节点一定是最优的。
同时,由于要计算截距最小值的的直线的斜率是 递增的,那么对于所有与后一点连线小于 的节点,在之后的统计中也不会用到了。
那么可以使用单调队列维护下凸壳,从队首弹出所有无用的节点,那么此时的队首就是最优解对应的节点。
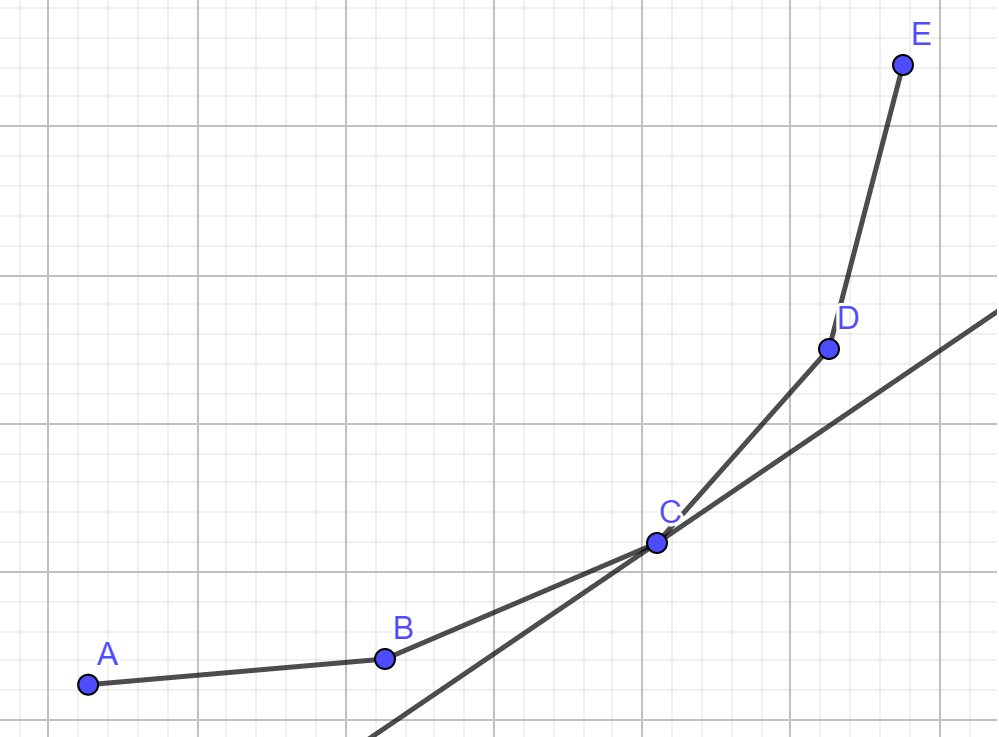
同时,在向队尾加入节点时,如果形成了上凸,那么要弹出原来的队尾节点,直到不存在上凸为止。
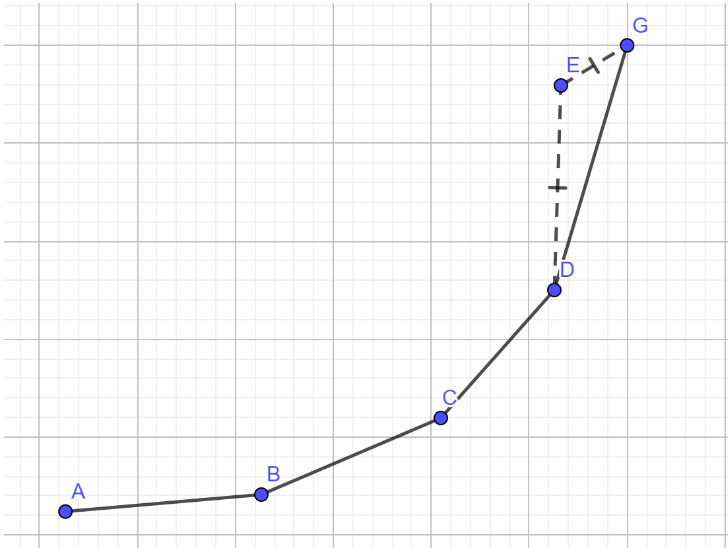
如图,插入 节点前需要弹出 节点,然后插入 点后再次形成下凸壳。
这就是基本的斜率优化模型,由于使用单调队列,每个元素至多出队入队一次,故时间复杂度为 .