基础微积分学习笔记

由于物理课要学习导数和定积分的内容，所以就写这样一篇学习笔记。内容十分基础，叙述十分不严谨。如有错误，还请指出。

⚠️警告：如果您真的想严谨、系统地学习微积分相关内容，请迅速关掉本文章，并找一本大学高数教材来看，避免被我误导。

不过大概也不会有这样的人

一、导数

1. 导数定义

导数的定义是当自变量的增量趋于零时，因变量的增量与自变量的增量之商的极限。一个函数在 $x_0$ 处的导数，是函数在该位置的变化率，也是函数在该位置的切线的斜率。当函数在 $x_0$ 处的导数为 0 时，说明函数在该点存在极值。

导函数就是函数的导数关于自变量的函数。

若函数 $f(x)$ 在 $x_0$ 处存在斜率，那么 $f(x)$ 在 $x_0$ 处的导数就为 $\lim\limits_{\Delta x \to 0}\dfrac{f(x_0+\Delta x)-f(x_0)}{\Delta x}=\dfrac{\mathrm d f(x_0)}{\mathrm d x_0}$ .

函数 $f(x)$ 的导函数记为 $f'(x)$，$f'(x)=\lim\limits_{\Delta x \to 0}\dfrac{f(x+\Delta x)-f(x)}{\Delta x} = \dfrac{\mathrm d f(x)}{\mathrm d x}$ .

通常来说，对一个函数求导是指求这个函数的导函数。

例：
求 $f(x)=x^3$ 的导数。

$\begin{aligned} & f'(x)\\ =\, &\lim\limits_{\Delta x \to 0}\dfrac{f(x+\Delta x)-f(x)}{\Delta x}\\ =\, &\lim\limits_{\Delta x \to 0}\dfrac{(x+\Delta x)^3-x^3}{\Delta x}\\ =\, &\lim\limits_{\Delta x \to 0}\dfrac{x^3+3x^2\Delta x+3x\Delta x^2+\Delta x^3 - x^3}{\Delta x}\\ =\, &\lim\limits_{\Delta x \to 0}(3x^2+3x\Delta x+\Delta x^2)\\ =\, &3x^2 \end{aligned}$

2. 基本初等函数导数公式及导数运算法则

(1). 基本初等函数导数公式

• 若 $f(x)=k$ ，则 $f'(x)=0$ ;
• 若 $f(x)=x^k$ ，则 $f'(x)=kx^{k-1}$ ;
• 若 $f(x)=\sin x$ ，则 $f'(x)=\cos x$ ;
• 若 $f(x)=\cos x$ ，则 $f'(x)=-\sin x$ ;
• 若 $f(x)=\tan x$ ，则 $f'(x)=\dfrac{1}{\cos^2x}$ ;
• 若 $f(x)=k^x$ ，则 $f'(x)=k^x\ln k$ ;
• 若 $f(x)=\log_k x$ ，则 $f'(x)=\dfrac{1}{x\ln k}$ .

(2). 导数运算法则

• 若 $f(x)=g(x)+h(x)$ ，则 $f'(x)=g'(x)+h'(x)$ ;
• 若 $f(x)=g(x)\cdot h(x)$ ，则 $f'(x)=g'(x)\cdot h(x)+h'(x)\cdot g(x)$ ;
• 若 $f(x)=\dfrac{g(x)}{h(x)}$ ，则 $f'(x)=\dfrac{g'(x)\cdot h(x)-h'(x)\cdot g(x)}{h^2(x)}$ ;
• 若 $f(x)=g(h(x))$ ，则 $f'(x)=g'(h(x))\cdot h'(x)$ .

例：
求 $f(x)=\sin(\cos(\tan x))$ 的导数。

分析：先设 $g(x)=\cos(\tan x)$ ，利用复合函数求导运算法则，求 $f(x)=\sin(g(x))$ 的导数，再求 $g(x)$ 的导数。

$\begin{aligned} & f'(x)\\=\, &\sin'(\cos(\tan(x)))\cdot (\cos(\tan(x)))'\\=\, &\sin'(\cos(\tan(x)))\cdot \cos'(\tan(x))\cdot \tan'(x)\\=\, &\cos(\cos(\tan(x)))\cdot (-\sin(\tan(x)))\cdot\dfrac{1}{\cos^2x}\\=\, &\dfrac{-\cos(\cos(\tan(x)))\cdot \sin(\tan(x))}{\cos^2x}\end{aligned}$

例：
求 $f(x)=x\sqrt{1-x^2}$ 的导数。

$\begin{aligned} &\; f'(x)\\=\, &x'\cdot \sqrt{1-x^2}+(\sqrt{1-x^2})'\cdot x\\=\, &\sqrt{1-x^2}+\dfrac{1}{2}(1-x^2)^{-\frac{1}{2}}\cdot (1-x^2)'\cdot x\\=\, &\sqrt{1-x^2}+\dfrac{-2x^2}{2\sqrt{1-x^2}}\\=\, &\dfrac{1-2x^2}{\sqrt{1-x^2}}\end{aligned}$

二、定积分

1. 定积分定义

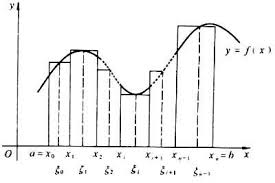
$f(x)$ 在实数区间 $[a,b]$ 上的定积分等于由曲线 $y=f(x)\ ,x\in [a,b]$ , 直线 $x=a$ , $x=b$ 和 x 轴围成的图形的面积。

把 $[a,b]$ 均分成 $n$ 份，设分点为 $x_0,x_1\cdots x_n$ , $\Delta x=\dfrac{b-a}{n}=x_i-x_{i-1},\ i\in[1,n]$ 。则长为 $\Delta x$ ，宽为 $f(x_i)$ 的矩形的面积 $S_i$ 与 $f(x)$ 在 $[x_i,x+\Delta x]$ 上的定积分的大小相近。且当 $\Delta x\to 0$ 时，矩形面积等于该部分定积分大小。故当 $\Delta x\to 0$ ，即 $n \to \infin$ 时，这 $n$ 个矩形的面积和就等于 $f(x)$ 在 $[a,b]$ 上的定积分。同时，当 $\Delta x \to0$ 时，任取 $\xi_i\in[x_i,x_{i+1}]$ ，都有 $S_i=f(\xi_i)\cdot\Delta x$.

把 $f(x)$ 在 $[a,b]$ 上的定积分记为 $\int_a^b f(x) \mathrm{d}x$ ，则有：

$\int_a^b f(x) \mathrm{d}x = \lim\limits_{n\to\infin}\sum_{i=1}^nf(\xi_i)\cdot \Delta x$

例：
求 $\int_0^1x^3\mathrm d x$.

由题，$\Delta x=\dfrac{1}{n}$ ，取 $\xi_i=\dfrac{i}{n}$ .

$\begin{aligned}&\int_0^1x^3\mathrm d x\\=\,&\lim\limits_{n\to\infin}\sum_{i=1}^n(\dfrac{i}{n})^3\cdot\dfrac{1}{n}\\=\,&\lim\limits_{n\to\infin}\dfrac{1}{n^4}\sum_{i=1}^ni^3\\=\,&\lim\limits_{n\to\infin}\dfrac{1}{n^4}\cdot\dfrac{1}{4}n^2(n+1)^2\\=\,&\lim\limits_{n\to\infin}\dfrac{1}{n^4}\cdot\dfrac{1}{4}n^2(n+1)^2\\=\,&\lim\limits_{n\to\infin}\dfrac{1}{4}(1+\dfrac{1}{n})^2\\=\,&\dfrac{1}{4}\end{aligned}$

由定积分定义，易得定积分以下性质：

• $\int_a^bkf(x)\mathrm{d}x=k\int_a^bf(x)\mathrm{d}x$ ;
• $\int_a^b[f(x)\pm g(x)]\mathrm{d}x=\int_a^bf(x)\mathrm{d}x\pm\int_a^bg(x)\mathrm{d}x$ ;
• $\int_a^bf(x)\mathrm{d}x=\int_a^cf(x)\mathrm{d}x+\int_c^bf(x)\mathrm{d}x,\ a<c<b$ .

2. 微积分基本定理

1). 不定积分

要说微积分积分定理，不得不先提到不定积分的概念。不定积分也叫反导函数，顾名思义，就是导数的反函数。 函数 $f(x)$ 的不定积分记为 $\int f(x)\mathrm d x$ .

那么就显然有不定积分运算法则如下：

注意到，各式中均带有常数 $C$ ，这是因为常数的导数为 0 ，故在进行导数的逆运算时要带一个常数。

2). 微积分基本定理

设 $\int f(x)=F(x)$，记 $F(b)-F(a)=\left.F(x)\right|_{a} ^{b}$ .

那么就有：

$\int_{a}^{b} f(x) \mathrm d x=\left.F(x)\right|_{a} ^{b}$

这个定理的重要意义在于描述了导数（或者可以说微分）和积分之间的关系，使定积分变得容易求了许多。

证明？不会

例：
求 $\int_0^1x^3\mathrm d x$.

$\begin{aligned}&\int_0^1x^3\mathrm d x\\=\,&\left.\int x^3\mathrm d x\right|_0^1\\=\,&\left.\dfrac{1}{4} x^4\right|_0^1\\=\,&\dfrac{1}{4}\end{aligned}$